当我最初写下这个标题的时候，没想过这个话题会引申的复杂程度超过了我闲言碎语科普的地步。就像当时曾经我的导师给我的两个课题，第一个是Kodaira嵌入定理的一个alternative证明方法，然后他看我有些犯怵，于是跟我说：

“我这里还有个相对比较简单的课题是关于测地线的内容，相对简单很多，比较没意思，看你了”

很自觉的我，接受了挑战，选择了alternative的证明。然而实际上这也确实差点把我逼入绝境，关于这个话题，会在后面的后面再慢慢去说。而今天的故事，是从测地线开始。

古典微分几何的开始就像拿着微积分把直线掰弯，但不像高中的解析几何一样（解析几何一定意义上更多是代数几何的一个开端），微分几何很多还是以立体几何为起点，研究空间的形式与位置的相关性逻辑。16 17年以前，学界对于代数几何的话题更热，反映到高考上也多以解析几何和数论相关的归纳法作为最后两道压轴题。而近几年看上去更多偏向于函数相关的分析学，尤其是今年三角函数其实可以引申下去的傅立叶分析相关的这些偏向于实变和概率论相关的题目，也多半和现在ai狂热很相关了。

跑题了，说回测地线。如果看很多科普视频，很多人都会说是因为欧氏几何的第五条公设是有问题的，平行线的定义不合理，甚至都没有人真的去看下欧氏几何第五条公设是什么。实际上欧几里得几何第五条公设原文是：

“That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.”

认真阅读原文，其实这里并没有对平行进行描述，实际上来说结合前四条而言，直接的断言是三角形内角和等于180度。在某种程度上，等价于平行公设，而如果我们把讨论点放在一张平面上，这是不言自明的公理是没任何问题的。

那么是什么有问题呢？问题在于弯曲。一条绳子可以做成任何一种形状，当我们在不减断绳子的前提下，任何一个形状的周长都可以用这根绳子的长度来计算。当然这里其实有个很有意思的小实验，也经常被用来戏耍民科，就是不停的折叠正方形的一个角，最终这个折叠线会看起来很像是一条直线，并且会荒谬的得出2=√2的结论，但事实其实也很简单，就是∑(1/n)并不收敛。直观上来看，当你有一个可以无限放大的小镜子，去看一个小片区域，你会发现总会有一个直角三角形在，而不是一个平滑的直线。折叠，更像是折断，在某种情况下折断打破了对象的整体属性，正如那句很有名的话：

可导一定连续，但连续不一定可导。

而上述的例子，其实更多还是想说，我们对于几何的研究，更多是服务于实际生产的，度量，测量长度，面积，角度。正如当年物理从低速世界像光速世界迈进一样，当大航海时代的开启，在前人的不断启发下，传统的欧式几何，在水手们知道地球是圆的时候，开始对测量位置和角度，产生了很多的问题。最重要的就是：

当我和另一艘船，分别从赤道的两个方向，沿着正北方向前行，我们终将会在北极点碰面。

那么问题来了，按照欧氏几何的定理，沿着赤道这条直线出发，我和另一艘船，都是垂直于赤道，那我俩原则上是永远不会相见的。此时其实欧氏几何的前四条公里依然成立，只是第五条，失效了。相较于可能大部分人会说的想在平面上画出一张等距的世界地图是无法实现的，我更喜欢用这条来说明问题。所以问题出在哪里，其实用一个比较不学术的词来说，就是形变（同胚），或者在说的通俗一些，就是如何弯曲。

数学的一个最好的点就在于，对于同样一个结论，当你尝试用不同的方法去研究，是会得出相同的结论。这是一个很trivial的论调，当然如果要去论证其实也又把哥德尔不完备来聊一遍，即在皮亚诺公理体系下存在不可证伪的伪命题一样。对于微分几何的发展，如果要追溯历史，不仅因为大航海时代对于地图测量的要求，基于电磁学的磁通量而更有用的第二类曲面积分也至关重要。微积分在最开始学习的时候都会被老师用求不规则曲线和坐标系围成的面积来讲解积分的过程，但其实这里没有强调一个很重要的点在于，微分和积分是一个逆运算。毕竟对于积分这么强大的工具，不仅仅只是去求一个面积。相信也只有数学系的老师会讲到这里就是，微积分最重要的，或者微积分基本定理是什么，其实每个人都知道，或者说，我认为牛顿之所为可以在物理之外的数学领域霸榜第一的原因只因为这个公式就是：

牛顿-莱布尼茨公式

牛顿-莱布尼茨公式给出的不仅仅是一个定积分的微分逆运算。他不仅仅只是一个计算公式，跳出这个公式认真观察，他最最最重要的点是告诉我们，在一个一维直线上，定义的一条曲线，这条曲线的形式，会和曲线两点的函数相关，而这个函数，正是这条曲线对应函数的积分形式。

这个描述还不够直观，因此也不够震撼。这里最关键的是打破了维度的限制，两个点是0维，而一条线是1维，结合三大中值定理，你不需要看到那条线的全貌，仅通过计算就可以了解到那条线的长度，最大值最小值，中间的停留点，等信息。

基于此，我们可以去计算一条弯曲曲线的长度（第一型曲线积分），当我们定义曲线的方向后，当我们定义了积分路径的方向，则也有了第二型曲线积分，也有了很重要的一个定理就是闭合环路的第二型曲线积分为0。

在这里为了让上述描述不具有跳跃性，各位看官还请脑补一段隐函数定理。

而来到电磁学的时候，麦克斯韦公式中的积分和微分形式，也更是展示着这个逆运算之间的伟大。我还记得曾经老师形容关于这类公式的一个很好的点就是。想象一个喷泉，喷泉的中心一个点在往外溢出水流。从边界溢出的水流量，就是中心喷出水填满这个面积后，多出去的部分。边界和内部，有着天然的联系。我们往往只需要边界的信息，就可以知道全貌的大概，而利用梯度，旋度，散度这些概念，我可没可以知道通过量，寻找极值，以及延展程度。还是当时老师的一句话，当处在群山之间被蒙住眼睛的我看不到全貌的时候，我拄着一根拐棍，每走一步我都用怪根四处梯度下降的方向，当我走到一个位置，四处都是梯度上升的时候，我一定在一个区域呢，找到了一个极值。

数学分析的最后几章，关于多元函数积分中的格林公式和高斯公式，一言以蔽之的话，就是二维和三维，对于牛顿莱布尼兹公式的扩张。他们做的最重要的事情，都是构建起了高一维曲面曲块与低一维曲线曲面之间的联系。

格林公式：

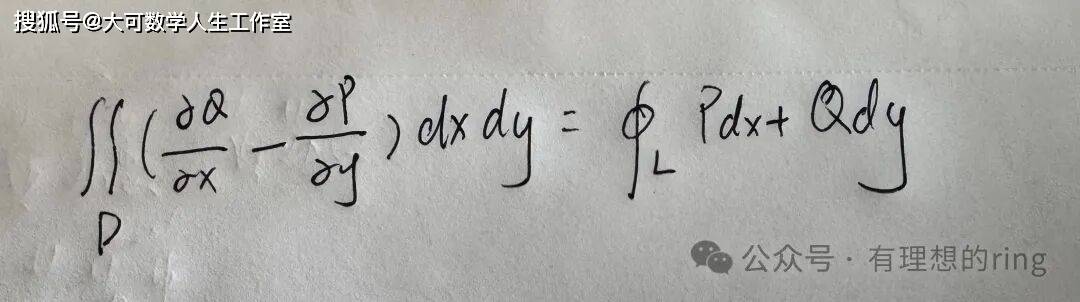
高斯公式

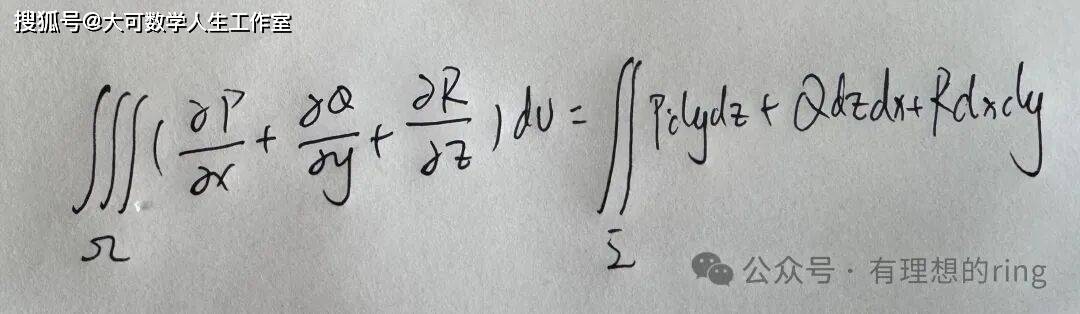
那这些和测地线有什么关系呢？本章的故事基本都是在科普，其实读到现在，我们从公元前古希腊年代的几何蛮荒，到近现代微积分，人类对于数学的探索从固定的简单形状，逐步走向了不规则的复杂形状，甚至是任意弯曲的形状。而对于现实世界的思考，也从静止的一次推动，走向了连续的世界。当人类开启大航海时代的篇章时，哥伦布和郑和站在船头眺望远方的时候，他们内心对于未知的探索谱写着人类进步的岁月史诗。海的那边是什么，当我一直走下去的时候，会走到世界的尽头么？而这些勇者背后，支撑他们的，也正是那一个又一个伏案埋头苦算的科学家们。测地线这一个看似简单的概念，却也承接了人类千年发展以来的探索与智慧的结晶。

作为本系列的开篇，我尝试用最通俗的语言，在有限的篇幅里（大家能接受的篇幅）每篇会控制在3000字以内。希望可以给大家带来一些小小的启发。也欢迎交流指正。